Essential length of roller chain
Making use of the center distance among the sprocket shafts and also the variety of teeth of each sprockets, the chain length (pitch variety) might be obtained through the following formula:
Lp＝（N1 ＋ N2）/2＋ 2Cp＋｛（ N2－N1 ）／2π｝2
Lp : Total length of chain (Pitch variety)
N1 : Number of teeth of tiny sprocket
N2 : Quantity of teeth of significant sprocket
Cp: Center distance concerning two sprocket shafts (Chain pitch)
The Lp (pitch number) obtained from your above formula hardly turns into an integer, and usually involves a decimal fraction. Round up the decimal to an integer. Use an offset website link if the quantity is odd, but select an even amount around attainable.
When Lp is established, re-calculate the center distance involving the driving shaft and driven shaft as described inside the following paragraph. When the sprocket center distance can not be altered, tighten the chain applying an idler or chain tightener .
Center distance amongst driving and driven shafts
Clearly, the center distance amongst the driving and driven shafts have to be far more compared to the sum of your radius of each sprockets, but in general, a right sprocket center distance is viewed as for being thirty to 50 instances the chain pitch. Even so, if your load is pulsating, 20 instances or significantly less is appropriate. The take-up angle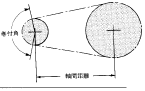 
in between the smaller sprocket and the chain has to be 120°or far more. When the roller chain length Lp is offered, the center distance among the sprockets could be obtained through the following formula:
Cp＝１/4Lp－(N1＋N2)/2+√(Lp－(N1＋N2)/2)^2－2/π2（N2－N1）^2
Cp : Sprocket center distance (pitch amount)
Lp : All round length of chain (pitch variety)
N1 : Amount of teeth of little sprocket
N2 : Variety of teeth of large sprocket
Chain Length and Sprocket Center Distance
Tags